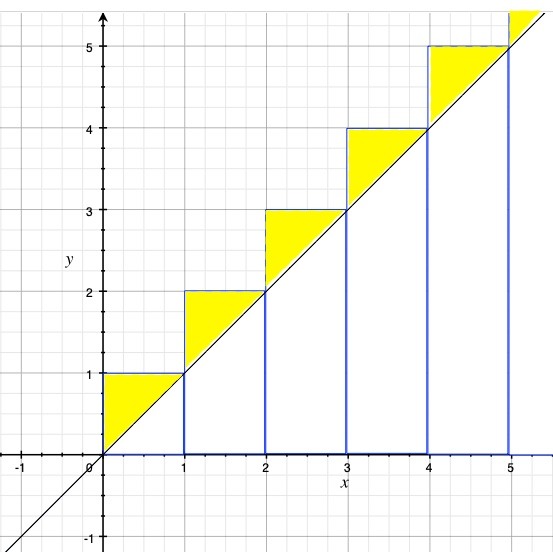
在第2課最後面提到的問題，1加到100的總和是5050，但是從方程式y = x來算三角形面積計算，卻只有5000，為什麼多出50? 這是因為1加到100並不是直接計算三角形面積，而是計算100個長條形的面積，也就是說：

1 + 2 + 3 + ⋯ + 100 = 1x1 + 2x1 + 3x1 + ⋯ + 100x1 （即每個長方形高=y, 寬=1）

所以每個長條形會多算0.5的面積，100個長條形剛好多出50的誤差，如下圖。

微積分的原理就是將長條形再細分，逐漸減少誤差，慢慢就趨近於實際三角形的面積。例如我們如果將長條形的寬從1縮短為0.5，誤差就會減半，如下圖。

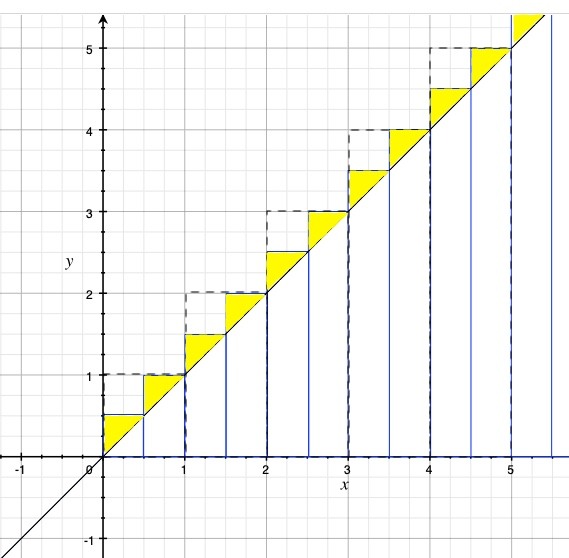
這樣的面積和，相當於以下算式：

0.5x0.5 + 1.0x0.5 + 1.5x0.5 + 2.0x0.5 + ⋯ + 99.5x0.5 + 100.0x0.5

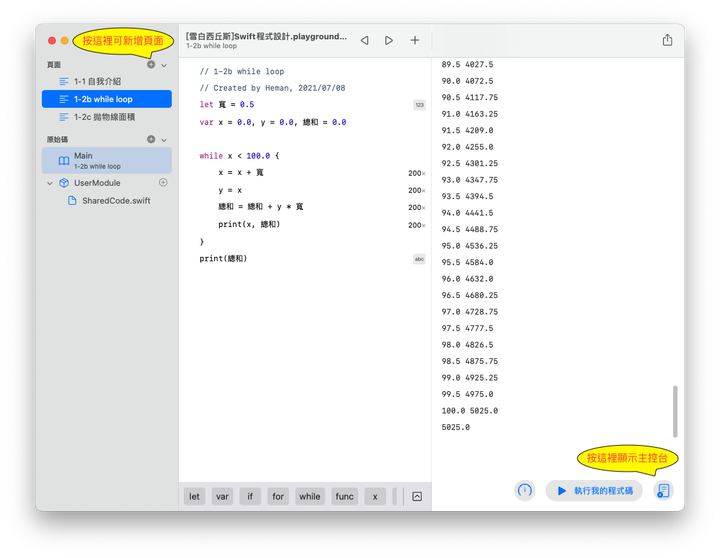
要如何用迴圈來計算呢？這次我們不用 for 迴圈，改用 Swift 另外一種 while 迴圈：

// 1-2b while loop
// Created by Heman, 2021/07/08
let 寬 = 0.5
var x = 0.0, y = 0.0, 總和 = 0.0

while x < 100.0 {
    x = x + 寬
    y = x
    總和 = 總和 + y * 寬
    print(x, 總和)
}
print(總和)

因為寬度（x軸的間隔）是固定的，因此用 let 設為常數。x, y以及總和設為變數，初始值歸零，這裡要注意用 0.0，代表實數，而不是整數 0。

接下來進入 while 迴圈：

while x < 100.0 { }

意思是「當x小於100.0時，執行 { } 裡面的指令」，注意用實數 100.0，不能用整數 100。計算結果總和是5025，誤差從50減少為25！同理，如果將程式中常數「寬」改為0.1，誤差又更小了，甚至改到0.01以下（但不能是0.0），直到誤差可以接受（例如誤差小於1）為止。

同樣的原理可以計算任何曲線的面積（近似值），例如下面的拋物線（二次方程式）:

y = 25 - (0.2*x - 5)²）